Question

A single​ 6-sided die is rolled twice. The set of 36 equally likely outcomes is​ {(1,1), (1,2),​ (1,3), (1,4), left parenthesis 1 comma 5 right parenthesis comma(1,5), left parenthesis 1 comma 6 right parenthesis comma(1,6), left parenthesis 2 comma 1 right parenthesis comma(2,1), left parenthesis 2 comma 2 right parenthesis comma(2,2), ​(2,3), (2,4),​ (2,5), (2,6),​ (3,1), (3,2),​ (3,3), (3,4),​ (3,5), (3,6),​ (4,1), (4,2),​ (4,3), left parenthesis 4 comma 4 right parenthesis comma(4,4), left parenthesis 4 comma 5 right parenthesis comma(4,5), left parenthesis 4 comma 6 right parenthesis comma(4,6), left parenthesis 5 comma 1 right parenthesis comma(5,1), left parenthesis 5 comma 2 right parenthesis comma(5,2), ​(5,3), (5,4),​ (5,5), (5,6),​ (6,1), (6,2),​ (6,3), (6,4),​ (6,5), (6,6)}. Find the probability of getting two numbers whose sum is greater than 9 and less than 13.

Answer 1

The probability of getting two numbers whose sum is greater than 9 and less than 13 is
`(1)/(6)`

Explanation:

Given : A single​ 6-sided die is rolled twice.

To find : The probability of getting two numbers whose sum is greater than 9 and less than 13 ?

Solution :

The set of 36 equally likely outcomes,

1 2 3 4 5 6

1 (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)

2 (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)

3 (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)

4 (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)

5 (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)

6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)

Getting two numbers whose sum is greater than 9 and less than 13

The favorable outcome is (4,6),(5,5),(5,6),(6, 4),(6, 5),(6, 6) = 6

The probability is given by,

`\text{Probability}=\frac{\text{Favorable Outcome}}{\text{Total Outcome}}`

`\text{Probability}=(6)/(36)`

`\text{Probability}=(1)/(6)`

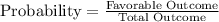
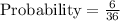
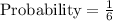
Therefore, The probability of getting two numbers whose sum is greater than 9 and less than 13 is
`(1)/(6)`