Answer:
48.2842 units is the perimeter of the parallelogram.
Explanation:
Area of the parallelogram = Base × Height
Base of the parallelogram,b = 10 units
Height of the parallelogram = h units
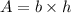
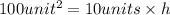
h = 10 units
In triangle , ABC
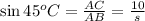
Side of the parallelogram AB = s =14.1421 units
Perimeter of parallelogram : 2(s+b) = 2(14.1421+10) units=48.2842 units.