Answer: 90.82%
Explanation:
Given : The distribution of the amount of a certain brand of soda in 16 OZ bottles is approximately normal .
Mean :
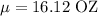
Standard deviation:

Let X be the random variable that represents the amount of soda in bottles.
Formula for z-score :

Z-score for 16 oz:
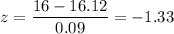
Using the standard normal z-distribution table , the probability that the soda bottles that contain more than the 16 OZ is given by :_
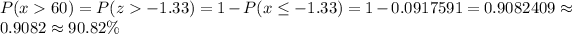
Hence, the percentage of the soda bottles that contain more than the 16 OZ advertised is 90.82% .