Question

Use differentials to estimate the amount of tin in a closed tin can with diameter 3 inch and height 4 inch, if the top and bottom are 0.02 inch thick and the side is 0.015 inch thick.

Answer 1

dv = 1.03 inch^3

Step-by-step explanation:

given data:

diameter = 3 inch

radius = 1.5 inch

height 4 inch

top and bottom thickness is 0.02 inch

side thickness = 0.015 inch

we know that volume of the cylinder is given as

`v  =\pi r^2 h`

by definition of differential we have

`dv =(\partial v)/(\partial r) dr + (\partial v)/(\partial h) dh`

where dh = -(0.02 + 0.02) = 0.04 inch [ sum of top and bottom thickness]

the radius is decreased by 0.02 inch, dr = 0.02 inc,

`(\partial v)/(\partial r)  = 2\pi r h = 37.69`

`(\partial v)/(\partial h) = \pi r^2 = 7.06`

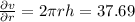
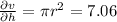
dv = 37.69*(0.02) + 7.06*(0.04)

dv = 1.03 inch^3