Question

A personal account earmarked as a retirement supplement contains $338,000. Suppose $300,000 is used to establish an annuity that earns 6%, compounded quarterly, and pays $6000 at the end of each quarter. How long will it be until the value of the annuity is $0

Answer 1

23.275 years

Step-by-step explanation:

Given:

Present value or the amount invested = $ 300,000

Rate = 6% compounded quarterly

i.e the rate of return quarterly will be = 6% / 4 = 1.5%

Quarterly payment = $ 6,000

Annuity = $ 0

Now,

Present value of annuity = Part payment × (
`(1-(1)/((1+r)^n))/(r)`)

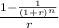where,

n is the number of quarters

on substituting the values in the formula, we get

$ 300,000 = $ 6000 × (
`(1-(1)/((1+(0.015))^n))/(0.015)`)

or

50 × 0.015 = (
`{1-(1)/((1.015))^n)`)

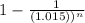or

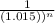`{(1)/((1.015))^n)` = 1 - 0.75

or

4 =
`(1.015)^n}`

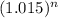
taking log both the sides

we get

log 4 = n × log 1.015

or

0.602 = n × 0.0064

or

n = 93.101 quarters

or

n = 93.101 / 4 = 23.275 years