Question

Write a paragraph proof.

Given: ∠T and ∠V are right angles.

Prove: ∆TUW ∆VWU

Answer 1

Explanation:

in ∆TUW & ∆VWU

∠UTW = ∠UVW (data / given)

WU = WU (common sides) ∠TWU = ∠VUW (TW//UV alternate∠ )

so ∆TUW & ∆VWU are congruent

Answer 2

∆TUW≅∆VWU by AAS.

Explanation:

Given information: ∠T and ∠V are right angles, TW║UV.

Prove: ∆TUW≅∆VWU

Proof:

If a transversal line intersect two parallel lines, then alternate interior angles are congruent.

In ∆TUW and ∆VWU,

`\angle T\cong \angle V` (Right angles)

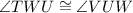`\angle TWU\cong \angle VUW` (Alternate interior angles)

`UW\cong UW` (Reflection property)

By AAS postulate, ∆TUW and ∆VWU are congruent.

`\triangle TUW\cong \triangle VWU`

Hence proved.