Question

1. A 6-cm-long guitar string is tuned to produce the note B3 (fundamental frequency 245 Hz). If the tension of the string is increase by 1%, what will be the change of the fundamental frequency of the string? a) 3.65Hz b) 4.85 Hz c) 2.44 Hz d) 1.22 Hz e) 5.34Hz

Answer 1

Change in the fundamental frequency of the string is 1.22 Hz.

Step-by-step explanation:

It is given that,

Length of string, l = 6 cm = 0.06 m

Fundamental frequency of the string, f = 245 Hz

If the tension of the string is increase by 1%, we need to find the fundamental frequency of the string. It is given by :

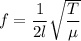`f=(1)/(2l)\sqrt{(T)/(\mu)}`.............(1)

Where

T is the tension in the string

`\mu` is mass per unit length

It is clear from equation (1) that the fundamental frequency is directly proportional to the tension in the string i.e.

`f\propto √(T)`

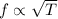
New tension, T' = 1.01 T

New frequency,
`f'=f* √(T)`

`f'=245* √(1.01)`

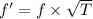
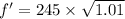
f' = 246.22 Hz

So, change in the fundamental frequency is given by :

`\Delta f=f'-f`

`\Delta f=246.22-245`

`\Delta f=1.22\ Hz`

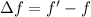
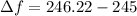
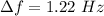
So, the change of the fundamental frequency of the string is 1.22 Hz. Hence, this is the required solution.