Question

A skater extends her arms horizontally, holding a 5-kg mass in each hand. She is rotating about a vertical axis with an angular velocity of one revolution per second. If she drops her hands to her sides, what will the final angular velocity (in rev/s) be if her moment of inertia remains approximately constant at 5 kg⋅m2, and the distance of the masses from the axis changes from 1 m to 0.1 m?

Answer 1

The answer is attached

Answer 2

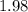`1.98` rev/s

Step-by-step explanation:

`m` = mass attached to each hand = 5 kg

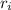`r_(i)` = initial distance of masses in each hand = 1 m

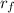`r_(f)` = final distance of masses in each hand = 0.1 m

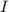`I` = moment of inertia of body = 5 kgm²

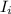`I_(i)` = initial total moment of inertia =
`I + 2 mr_(i)^(2)`

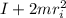
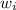`w_(i)` = initial angular velocity = 1 rev/s

`I_(f)` = final total moment of inertia =
`I + 2 mr_(f)^(2)`

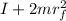
`w_(f)` = final angular velocity = ?

Using conservation of angular momentum

`I_(i) w_(i) = I_(f) w_(f)`

`(I + 2 mr_(i)^(2)) w_(i) = (I + 2 mr_(f)^(2)) w_(f)`

`(5 + 2 (5) (1)^(2)) (1) = (5 + 2 (5) (0.1)^(2)) w_(f)`

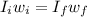
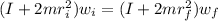
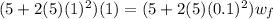
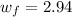`w_(f) = 2.94` rev/s