Answer:
(a). 90±45 km/hr
(b). 55.926 ± 2.7963 mil/hr
Step-by-step explanation:
Given that,
Uncertainty = 5.0%
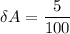
Here, A = 90 km/h
(a). We need to calculate the range of speed
We need to calculate the error of 5.0% uncertainty

Here,
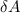 = uncertainty
= uncertainty
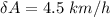
(b). We need to convert this range to miles per hour
1 km = 0.6214 mil
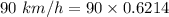
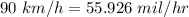

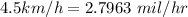
Hence, This is the required solution.