Question

The popularity rate of a political candidate is 52%. If 18 citizens are randomly selected, what is the probability that more than 12 in the sample are in favor of this candidate?

Answer 1

Answer)

The probability is 0.068

Explanation)

We shall use the binomial distribution to evaluate the problem

The probability that an event X occurs exactly 'r' times in 'n' trails is given by

`P(E)=\binom{n}{r}p^(r)(1-p)^((n-r))`

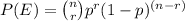
where 'p' is the probability of success of the event E

In the given case

p = 0.52

n = 18

Thus the probability that more than 12 people like the political candidate is

the probability that 13 or 14 or 15 or 16 or 17 or 18 people like the politician thus is given by values of 'r' belonging to the set {13,14,15,16,17,18}

`P(X>12)=P(13)+P(14)+P(15)+P(16)+P(17)+P(18)`

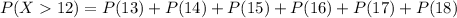
Applying values we get

`P(E)=P(X>12)=\binom{18}{13}(0.52)^(13)(1-0.52)^(18-13)+\binom{18}{14}(0.52)^(14)(1-0.52)^(18-14)+....+\binom{18}{18}(0.52)^(18)(1-0.52)^(18-18)`

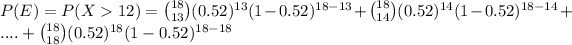
Thus P(E) = 0.068