Question

On a 10-item test, three students in Professor Hsin's advanced chemistry seminar received scores of 2, 5, and 8, respectively. For this distribution of test scores, the standard deviation is equal to the square root of A) 4. B) 5. C) 6. D) 9

Answer 1

D) 9

Explanation:

Standard Deviation is Calculated by formula:

`Standard deviation(\sigma) = Standard deviation(\sigma) = \sqrt{(1)/(n-1)\sum_(i=1)^(n){(x_(i)-\bar{x})^(2)} }`

where,
`\bar{x}` is mean of the distribution.

First: Calculating Mean of 2, 5 and 8:

`\text{Mean}(\bar x)=(2+5+8)/(3) = 5`

Then Standard deviation is:

`Standard deviation(\sigma) = \sqrt{(1)/(3-1)\sum_(i=1)^(n){(x_(i)-5)^(2)} }`

⇒
`\sigma = \sqrt{(1)/(2)[{(2-5)^(2)}+{(5-5)^(2)}+{(8-5)^(2)} } =\sqrt 9`

Answer 2

For this distribution of test scores, the standard deviation is equal to the square root of 9

D) 9

Explanation:

We need to know the standard deviation formula:

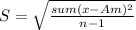`S=\sqrt{(sum(x-Am)^2)/(n-1) }` (1)

Where:

S: Standard deviation

sum: Summation

x: Sample values

Am: Arithmetic mean

n: Number of terms, in this case 3

Now, we need to know the arithmetic mean of the sample values: 2, 5 and 8

`Am=(2+5+8)/(3) = 5`

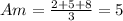
To know the standard deviation we need to have the summation of each term minus the arithmetic mean squared.

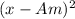`(x-Am)^2` of each term:

`(2-5)^2=9\\(5-5)^2=0\\(8-5)^2=9`

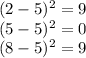
Now, we can find the standard deviation:

`S=\sqrt{(9+0+9)/(3-1) } \\S=\sqrt{(18)/(2) } \\S=√(9)`

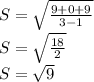
The standard deviation is equal to the square root of 9