Question

A man is building a gazebo and plans to use for the floor two boards that are 8 and three fourths feet ​, four boards that are 13 and five eighths feet ​, and two boards that are 6 one half feet. Find the total number of feet in all the boards.

Answer 1

The total number of feet in all the boards is 90 and 5/6 feet

Explanation:

First, it is necessary to transform the mixed number into a fraction. This can be made following the next rule:

`a(b)/(c) = ((a*c) + b)/(c)`

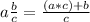
So, the number 8 and three fourth feet is equal to:

`8(3)/(4) = ((8*4) + 3)/(4) = (35)/(3)`

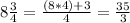
That means that we two boards that are 35/3 feet. So, multiplying 2 by 35/3 we get the total feets for the first type of board. That is:

`2*(35)/(3) = (2*35)/(3) =(70)/(3)`

At the same way, we can calculate the total number of feet for the second and third type of board as:

• Four boards that are 13 and five eighths feet:

`13(5)/(8) = ((13*8) + 5)/(8) = (109)/(8)`

`4*(109)/(8) = (4*109)/(8) =(109)/(2)`

• Two boards that are 6 one half feet:

`6(1)/(2) = ((6*2) + 1)/(2) = (13)/(2)`

`2*(13)/(2) = (2*13)/(2) =13`

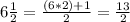
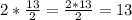
Finally, to find the total number of feet in all the boards, we need to sum the total number of feet for every type as:

`(70)/(3) +(109)/(2) +(13)/(1) =(545)/(6)`

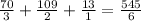
Converting this number to a mixed number we get:

`(545)/(6) =90(5)/(6)`

Because, when we divide 545 by 6, we get 90 as a quotient, 5 is the remainder and 6 is the divisor.