Answer:
10.5 small boxes equals the same amount of cereal in a large box
Step-by-step explanation:
see the attached figure to better understand the problem
Let
n is the number of smaller boxes
we know that
The equations
12 + 7.6n and 6 + 8n
are both representative of the amount of cereal that the new larger box contains
so
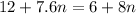
Solve for n
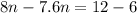
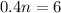

so
The amount of cereal in a large box is
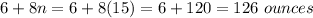
Remember that the amount of cereal in the smaller box is 12 ounces (see the attached figure)
so
Divide the volume of the larger box by the volume of the smaller box
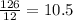
therefore
10.5 small boxes equals the same amount of cereal in a large box