Answer:
The value of the provide equation for x is
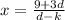 .
.
Explanation:
Consider the provided equation.
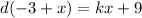
We need to solve the equation for x.
Use the distributive property:
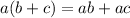
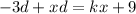
Subtract kx from both sides.
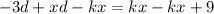
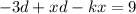
Add 3d both sides.
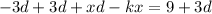
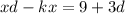
Take x common from left side.
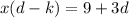
Divide both the sides by d-k.
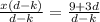
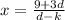
Hence, the value of the provide equation for x is
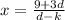 .
.