Question

The acceleration of a particle is defined by the relation a 5 28 m/s2. Knowing that x 5 20 m when t 5 4 s and that x 5 4 m when v 5 16 m/s, determine (a) the time when the velocity is zero, (b) the velocity and the total distance traveled when t 5 11 s.

Answer 1

Step-by-step explanation:

It is given that,

The acceleration of a particle,
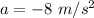`a=-8\ m/s^2` (negative as the particle is decelerating)

Initial distance, x₁ = 20 m

Initial time, t₁ = 4 s

New distance x₂ = 4 m

Velocity, v = 10 m/s

(A) Calculating initial distance using second equation of motion as :

`x_1=ut_1+(1)/(2)at^2`

`20=4u+(1)/(2)(-8)* 4^2`

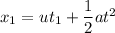
u = 21 m/s

When velocity of the particle is zero, time taken is t (say). Using first equation of motion as :

`v=u+at`

`0=21+(-8)t`

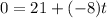
t = 2.62 seconds

So, the velocity of the particle is zero at t = 2.62 seconds.

(B) Velocity at t = 11 s

`v=21+(-8)* 11`

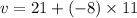
v = 13 m/s

Total distance covered at t = 11 s. The overall path travelled by the particle during its entire journey is called total distance covered.

`d=ut+(1)/(2)at^2+|ut+(1)/(2)at^2|`

`d=21* 2.62+(1)/(2)* (-8)(2.62)^2+|21* 8.38+(1)/(2)* (-8)(8.38)^2|`

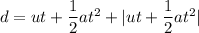
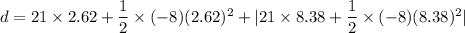
d = 132.48 m

So, the distance travelled by the particle at t = 11 seconds is 132.48 meters.