Question

Seven members of a Girl Scout troop report the following individual earnings from their sale of candy: $4, $1, $7, $6, $8, $2, and $7. In this distribution of individual earnings. (A) the mean is less than the mode and equal to the median.(B) the mean is less than the mode and less than the median.(C) the mean is equal to the mode and equal to the median.(D) the mean is greater than the mode and greater than the median.(E) the mean is equal to the mode and greater than the median.

Answer 1

(B) the mean is less than the mode and less than the median.

Explanation:

Mean, Median, Mode is used to calculate the central tendency of the distribution.

Mean is defined as,

`Mean = (Sum of all observation)/(Total number of observation)\\ \ \ \ \ \ \ \ \ = (4+1+7+6+8+2+7)/(7)`

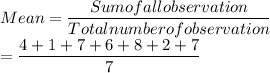
∴ Mean = 5

Median is the middle observation of the distribution after arranging it in ascending or descending order.

So, arranging distribution in ascending order we get,

$1, $2, $4, $6, $7, $7, $8

Also, a number of observation is 7 which is an odd number.

Hence,
`Median = ((Number of observation + 1)/(2))^(th) term`

⇒
`Median = ((7 + 1)/(2))^(th) term`

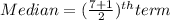
⇒ Median = 4th term = 6

Mode is the observation which has highest frequency.

Here, only $7 is repeated 2 times.

Hence, Mode = 7.

Hence, we see that Mean < Median < Mode

So, Option (B) is correct i.e. mean is less than the mode and less than the median.