Answer: 1.300228
Explanation:
We know that the t-score for a level of confidence
 is given by :_
is given by :_
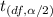 , whre df is the degree of freedom and
, whre df is the degree of freedom and
 is the significance level.
is the significance level.
Given : Level of significance :

Then , significance level :
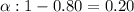
Since , sample size :
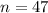
Degree of freedom for t-distribution:
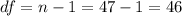
With the help of the normal t-distribution table, we have
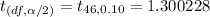
Hence, the t-score should be used to find a 80% confidence interval estimate for the population mean = 1.300228