Question

​A sample is selected from a population with μ = 46 and a treatment is administered to the sample. After treatment, the sample mean is M = 48 with a sample variance of s2 = 16. Based on this information, the size of the treatment effect, as measured by Cohen’s d, is ____.

Answer 1

0.125

Explanation:

Cohen's d is used to measure the effect size. Larger the value of Cohen's d, larger the effect between two observations.

It is determined by the formula,

`d= (M_(2)-M_(1))/(Standard deviation)`

where M₂ is Mean of 1st group

M₁ is the Mean of the 2nd group.

Here, M₁ = 46, M₂ = 48 and Standard deviation = 16

∴
`d= (48-46)/(16)`

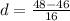
⇒ d = 0.125