Answer:
The NPV of the project at 8.7 percent will be 4,802.58
Step-by-step explanation:
We will calcualte the present value of the cash inflow:
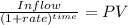
year 3:
Inflow 11,900.00
time 3.00
rate 0.087
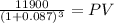
PV 9,265.28
Year 4:
Inflow 11,900.00
time 4.00
rate 0.087
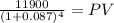
PV 8,523.71
Year 6:
Inflow 50,500.00
time 6.00
rate 0.087
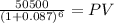
PV 30,613.58
Then, we will add them together and subtract the investment amount
NPV: 30,613.59 + 8,523.71 + 9,265.28 - 43,600 = 4,802.58