Question

Determine the point estimate of the population proportion, the margin of error for the following confidence interval,and the number of individuals in the sample with the specified characteristic, x,for the sample size provided.Lower bound=0.226,upper bound=0.604,n=1200The point estimate of the population is? round to the nearest thousandth as needed.the margin error is? round to the nearest thousandth as needed .the number of individuals in the sample with the specified characteristic is? round to the nearest integer as needed.

Answer 1

Answer: The point estimate of the population is 0.415 round to the nearest thousandth as needed.the margin error is 0.189 .

Explanation:

Let
`\overline{x}` be the sample mean .

We know that the confidence interval for population mean is given by :-

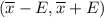`(\overline{x}-E,\overline{x}+E)`, where E is the margin of error .

Given : Lower bound of the confidence interval = 0.226

Upper bound of the confidence interval =0.604

i.e.

`\overline{x}-E=0.226------(1)\\\\\overline{x}+E=0.604--------------(2)`

Adding (1) from (2), we get

`2\overline{x}=0.83\\\\\Rightarrow\ \overline{x}=0.415`

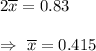
From (2),

`0.415+E=0.604\\\\\Rightarrow\ E=0.604-0.415=0.189`

Hence, the point estimate of the population is 0.415 round to the nearest thousandth as needed.the margin error is 0.189 .