Question

A Ferris wheel boarding platform is 3 meters above the ground, has a diameter of 80 meters, and makes one full rotation every 10 minutes. How many minutes of the ride are spent higher than 48 meters above the ground?

Answer 1

The answer is 4.6 minutes

Explanation

First we have to calculate the arc length of the ferris wheel that is higher than 48 metters, knowing that the center of the wheel is 43 m over the ground (3 meters of the platform and 40 meters of the radius). So to calculate the ends of the arc, we need to know the angle
`\alpha` between the horizontal radius at 43 meters and the one that reaches 48 meters. We can use the definition of the sine function

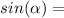`sin(\alpha ) =` Opposite cathetus / Hypotenuse

where the opposite cathetus is equal to the five meters missing from the center of the ferris wheel to the required height, and the Hypotenuse is equal to the radius. Then solving for alpha,

`\alpha =sin^(-1)(5 m/40 m) = 0.125 rad`

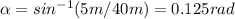
so the arc length higher than 48 meters is equal to the half circumference minus twice the arc length formed by the radius of the ferris wheel at an
`\alpha` angle.

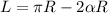`L = \pi R - 2\alpha R` = 115.66 m.

Now considering a rotation of one turn every 10 minutes in terms of arc length and a cross-multiplication.

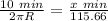
`(10\ min)/(2\pi R ) = (x\ min)/(115.66)`

`x \min= 4.6`.