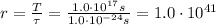Question

How many top quark lifetimes have there been in the history of the universe (i.e., what is the age of the universe divided by the lifetime of a top quark)? Note that these powers of 10 follow the same rules that any exponents would follow.

(The age of the universe is around 100,000,000,000,000,000s. A top quark has a lifetime of roughly 0.000000000000000000000001s. Writing numbers out with all these zeros is not very convenient. Such quantities are usually written as powers of 10. The age of the universe can be written as 1017s and the lifetime of a top quark as 10−24s.
Note that1017 means the number you would get by multiplying 10 times 10 times 10... a total of 17 times. This number, as you can see above, would be a one followed by seventeen zeros. Similarly, 10−24 is the result of multiplying 0.1 (or 1/10) times itself 24 times. As seen above, this is written as 23 zeros after the decimal point followed by a one.)

Answer 1

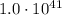`1.0\cdot 10^(41)` times

Step-by-step explanation:

First of all, we need to write both the age of the universe and the lifetime of the top quark in scientific notation.

Age of the universe:

`T=100,000,000,000,000,000s = 1.0\cdot 10^(17) s` (1 followed by 17 zeroes)

Lifetime of the top quark:

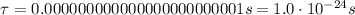`\tau = 0.000000000000000000000001s = 1.0\cdot 10^(-24) s` (we moved the decimal point 24 places to the right)

Therefore, to answer the question, we have to calculate the ratio between the age of the universe and the lifetime of the top quark:

`r = (T)/(\tau)=(1.0\cdot 10^(17) s)/(1.0\cdot 10^(-24) s)=1.0\cdot 10^(41)`