Answer:
1.
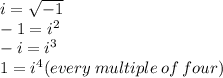
2.
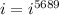
Explanation:
3. After i⁴, the cycle repeats itself from the very beginning [i = i⁵ (and so on)]. Every 4⁄4 that go by, you start from the beginning, but you keep moving up one in the exponents.
2. Since ¼ of 5689 is 1422¼, I know that it is imaginary, or iota, so moving one down would give 5688, where ¼ of that is 1422, with NOTHING left over, and that would equal to 1. You see, you have to know your multiples and divisiblity rules. The divisiblity rule of 4 states that if the LAST TWO DIGITS of an entire number are divisible by 4, then the ENTIRE number is divisible by 4. So, from this, you can tell how to answer this.
1. The pattern is in the above answer. ↑
** This can also include NEGATIVE EXPONENTS.
I hope this helps you out alot, and as always, I am joyous to assist anyone at any time.