Question

4. Two thin plano-convex lenses have their curved surfaces with the same radius of curvature equal to 5 cm each. Lens 1 has a focal length f1 = 10 cm and lens 2 has a focal length f2 = 12 cm. Find the ratio n1/n2 of the indices of refraction of these two lenses. a) 1.105 b) 1.083 c) 1.059. d) 1.125 e) 1.133

Answer 1

The ratio of the indices of refraction of these two lenses is 1.059.

(c) is correct option.

Step-by-step explanation:

Given that,

Radius of curvature = 5 cm

Focal length of first lens= 10 cm

Focal length of second lens = 12 cm

We need to calculate the ration of the indices of refraction of these two lenses

We need to calculate the indices of refraction of first lens

Using formula of focal length for first lens

`(1)/(f_(1))=(n_(1)-1)((1)/(R_(1))-(1)/(R_(2)))`

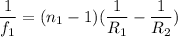
Here,
`R_(1)=\infty`

`R_(1)=-5`

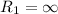
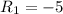
Put the value into the formula

`(1)/(10)=(n_(1)-1)((1)/(\infty)-(1)/(-5))`

`(1)/(10)=(n_(1)-1)(0-(1)/(-5))`

`n_(1)=(1)/(2)+1`

`n_(1)=1.5`

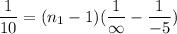
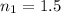
We need to calculate the indices of refraction of second lens

Using formula of focal length for first lens

`(1)/(f_(2))=(n_(2)-1)((1)/(R_(1))-(1)/(R_(2)))`

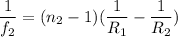
Put the value into the formula

`(1)/(12)=(n_(2)-1)((1)/(\infty)-(1)/(-5))`

`(1)/(12)=(n_(2)-1)(0-(1)/(-5))`

`n_(2)=(5)/(12)+1`

`n_(2)=1.416`

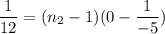
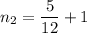
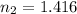
The ratio of the indices of refraction of these two lenses.

`(n_(1))/(n_(2))=(1.5)/(1.416)`

`(n_(1))/(n_(2))=1.059`

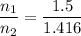
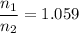
Hence, The ratio of the indices of refraction of these two lenses is 1.059.