Question

F $1,000 is deposited in a certain bank account and remains in the account along with any accumulated interest, the dollar amount of interest, I, earned by the deposit in the first n years is given by the formula

I = 1,000 ( (1 + r/100)^n - 1 ),

where r percent is the annual interest rate paid by the bank. Is the annual interest rate paid by the bank greater than 8 percent?

(1) The deposit earns a total of $210 in interest in the first two years.
(2) ( 1 + r/100 )^2 > 1.5

Answer 1

(1) The annual interest rate is 10%, that is greater than 8%

(2) The annual interest is bigger than 22.47% and that is greater than 8%

Explanation:

We have the equation:

`I=1,000((1+(r)/(100) )^(n) -1)`

Where I is the earns in interest, n is the number of years and r is the annual interest rate.

For the first case, we can replace I by $210 and n by 2 as:

`210=1,000((1+(r)/(100) )^(2) -1)`

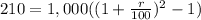
Solving for r, we get:

`(210)/(1,000) = (1+(r)/(100))^(2) -1`

`0.21 +1 = (1+(r)/(100))^(2)`

`1.21 = (1+(r)/(100))^(2)`

`√(1.21) = 1 + (r)/(100)`

`√(1.21) - 1 = (r)/(100)`

`(√(1.21) - 1)100=r`

`10=r`

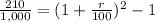
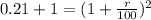
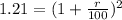
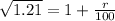
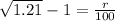
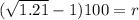
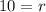
So, for the first case, the interest rate paid by the bank is 10% and it is greater than 8%

For the second case, we need to take the equation and solve for r as:

`(1+(r)/(100) )^(2) >1.5`

`1+(r)/(100) > √(1.5)`

`(r)/(100) > √(1.5)-1`

`r > (√(1.5)-1)*100`

`r > 22.47`

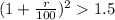
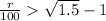
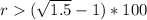
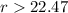
So, for the second case the rate need to be bigger than 22.47% and that is bigger than 8%