Question

Pumps A, B, and C operate at their respective constant rates. Pumps A and B, operating simultaneously, can fill a certain tank in 6/5 hours; pumps A and C, operating simultaneously, can fill the tank in 3/2 hours; and pumps B and C, operating simultaneously, can fill the tank in 2 hours. How many hours does it take pumps A, B, and C, operating simultaneously, to fill the tank? A. 1/3 B. 1/2 C. 2/3 D. 5/6 E. 1

Answer 1

The correct option is E.

Explanation:

It is given that pumps A and B, operating simultaneously, can fill a certain tank in 6/5 hours.

One hour work of A and B = 5/6

Pumps A and C, operating simultaneously, can fill the tank in 3/2 hours.

One hour work of A and C = 2/3

Pumps B and C, operating simultaneously, can fill the tank in 2 hours.

One hour work of B and C = 1/2

We need to find the how many hours does it take pumps A, B, and C, operating simultaneously, to fill the tank.

Add one hour work

A and B + A and C + B and C =
`(5)/(6)+(2)/(3)+(1)/(2)`

`2A+2B+2C=(5+4+3)/(6)`

`2(A+B+C)=(12)/(6)`

`2(A+B+C)=2`

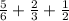
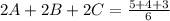
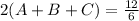
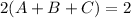
Divide both sides by 2.

`(A+B+C)=1`

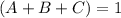
Reciprocal of 1 is 1. It means ABC can fill the tank in 1 hour simultaneously. Therefore the correct option is E.