Question

Suppose that the hourly wages of fast food workers are normally distributed with an unknown mean and standard deviation. The wages of 40 randomly sampled fast food workers are used to estimate the mean wage of the population. What t-score should be used to find the 80% confidence interval for the population mean?

Answer 1

Answer: 1.303639

Explanation:

The t-score for a level of confidence
`(1-\alpha)` is given by :_

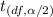`t_((df,\alpha/2))`, where df is the degree of freedom and
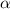`\alpha` is the significance level.

Given : Level of significance :
`1-\alpha:0.80`

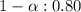
Then , significance level :
`\alpha: 1-0.80=0.20`

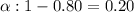
Sample size :
`n=40`

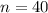
Then , the degree of freedom for t-distribution:
`df=n-1=40-1=39`

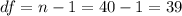
Using the normal t-distribution table, we have

`t_((df,\alpha/2))=t_(39,0.10)=1.303639`

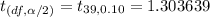
Thus, the t-score should be used to find the 80% confidence interval for the population mean =1.303639