Answer:
The score corresponds to the 95.82th percentile.
Step-by-step explanation:
To formula to calculate the percentile in a normal distribution is:
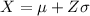
Where
 is the value of the variable,
is the value of the variable,
 is the mean,
is the mean,
 is the value from the standard normal distribution for the percentile. In this case, you have
is the value from the standard normal distribution for the percentile. In this case, you have
 and want to know the value of
and want to know the value of
 .
.
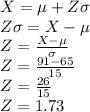
The value of
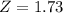 in the table of the standard normal distributions gives a value of 0.9582, which means the score is in the 95.82th percentile.
in the table of the standard normal distributions gives a value of 0.9582, which means the score is in the 95.82th percentile.