Question

Consider the expression
`2 \pi \sqrt{(l)/(g)}`.

where ℓ is length and g is gravitational acceleration in units of length divided by time squared.
Evaluate its units.
1. s²
2.
`((s)/(m))^2`
3.
`((m)/(s))^2`
4.
`(m)/(s)`
5. s
6. m²
7. m
8.
`(s)/(m)`

Answer 1

The expression 2π√(l/g) has units of 2π(l/g)^(1/2).

Step-by-step explanation:

The given expression is 2π√(l/g), where ℓ represents length and g represents gravitational acceleration in units of length divided by time squared. To evaluate the units of the expression, we need to break it down step by step:

The square root of a unit is equal to the unit raised to the power of 1/2. Therefore, the square root of (l/g) would have units of (l/g)^(1/2). Multiplying 2π by (l/g)^(1/2) would result in units of 2π(l/g)^(1/2). Finally, the (√) symbol represents the square root, so (√(l/g)) would have units of (l/g)^(1/2). Therefore, the expression 2π√(l/g) has units of 2π(l/g)^(1/2).

Answer 2

Step-by-step explanation:

lets start from the expression
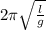`2\pi \sqrt{(l)/(g) }`, first remember that
`2\pi` is a constant with no units, so we do not need to consider it for this problem, so lets just think about
`(l)/(g)`

Next lets replace the units, l is the length which is represented in metters by international units system

g is the gravitational constants, so the units are lengt divided by time squared, since time is in seconds we have
`(m)/(s^(2) )`

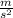
so pluging that into our formula we have
`\sqrt{(m)/((m)/(s^(2) ) ) }`

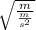
Now see we are dividing by a fraction, remember that to divide by a fraction is the same as to multiply by the reciprocal fraction, so we just flip the fraction and we get
`\sqrt{m*(s^(2) )/(m) }`

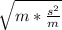
then if we perform the multiplication we have inside the radical we get
`\sqrt{(m*s^(2) )/(m) }`

Then since we are multiplying and dividing by m, the m's just cancel and we have
`\sqrt{s^(2) }`

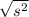
Now remember that square and square root are inverse operations, so they cancel each other and we are left with just
`s`, which means seconds, so the answer would be option 5

hope that helps, good bye :)