Question

Find the measure of angle J, the smallest angle in a triangle with sides measuring 11, 13, and 19. Round to the nearest whole degree

Answer 1

34 degrees

Explanation:

hope this helps

Answer 2

34°

Explanation:

We need to use the law of cosines to find angle J.

`11^(2)=19^(2) +13^(2) -2(19)(13)cos(J)\\121=361+169-494cos(J)\\121=530-494cos(J)\\121-530=-494cos(J)\\-409=-494cos(J)\\cos(J)=(-409)/(-494) \approx 0.8\\ J \approx cos^(-1)((409)/(494) ) \approx 34\°`

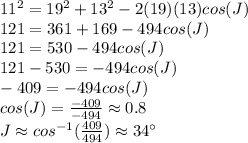
Therefore, the right answer is the second choice, 34°.

Remember, when you apply the law of cosines, the first square in the formula must be the opposite side to the angle we want to find.