Question

Assume that you are considering the purchase of a 20-year, noncallable bond with an annual coupon rate of 9.5%. The bond has a face value of $1,000, and it makes semiannual interest payments. If you require an 10.7% nominal yield to maturity on this investment, what is the maximum price you should be willing to pay for the bond?

Answer 1

The price I´d be willing to pay for this bond is $901.7954

Step-by-step explanation:

First we have to transform the data to useful information.

Coupon rate.

Since the coupon rate is annual but the bond pays semi-annual payments, we have to transform this annual coupon into a semi-annual coupon, that is:

C(semi-annual) = 9.5%/2 = 4.75%

C($) = 4.75% x 1000 = $47.5 every semester

We can do this since a coupon rate is both, nominal and effective.

Require nominal rate yield

This is our discount rate and it has to be an effective rate in order to discount all positive cash flows to present value (in our case, we will use the formula of an uniform annuity, we still need it effective).

This discount rate is nominal.

Discount rate = 10.7% Annual, semi-annual, due

this means that every year, payments are going to be made every 6 months, at the end of every 6 months, therefore to transform this nominal rate into an effective rate, we would have to divide it by 2.

Discount rate = 10.7% / 2 = 5.35% effective annually

now, we have to bring to present value all the positive cash flows.

`Present Value =(Coupon((1+r)^((n-1)) -1) )/(r(1+r)^((n-1)) ) +(Face Value+Coupon)/((1+r)^(n) )`

`Present Value =(47.5((1+0.0535)^(39) -1) )/(0.0535(1+0.0535)^(39) ) +(1000+47.5)/((1+0.0535)^(40) )`

`Present Value = 771.55+130.25=901.7954`

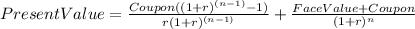
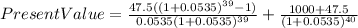
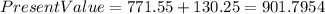
Notice that I used 4 digits after "." it should be even more, but I thought I would look bad, I hope you get the idea.

Best of luck