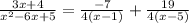Answer:
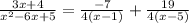
Explanation:
The given rational expression is:
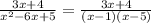
We can use concept of Partial Fractions to solve this problem. Let,
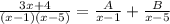
Multiplying both sides by (x - 1)(x - 5), we get:
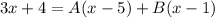
Substituting x = 5, we get:
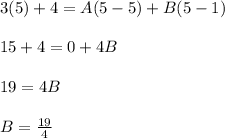
Substituting x = 1, we get:
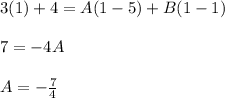
Substituting the value of A and B, back in the original equation, we get: