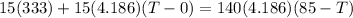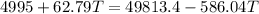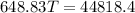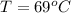Question

An insulated Thermos contains 140 cm3 of hot coffee at 85.0°C. You put in a 15.0 g ice cube at its melting point to cool the coffee. By how many degrees has your coffee cooled once the ice has melted and equilibrium is reached? Treat the coffee as though it were pure water and neglect energy exchanges with the environment. The specific heat of water is 4186 J/kg·K. The latent heat of fusion is 333 kJ/kg. The density of water is 1.00 g/cm3.

Answer 1

`T = 69^o C`

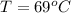
Step-by-step explanation:

Here at thermal equilibrium we can say that thermal energy given by Hot coffee is equal to the thermal energy absorbed by ice cubes

So here we have

`Q_(ice) = Q_(coffee)`

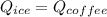
now since ice cubes are added into coffee when it is at melting temperature

So here we can say that final temperature of coffee is T degree C

Now we have

`m_1L + m_1c_1\Delta T_1 = m_2c_2\Delta T_2`

here we have

`m_1 = 15 gram`

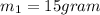
L = 333 kJ/kg = 333 J/g[/tex]

`c_1 = c_2 = 4186 J/kg C = 4.186 J/g C`

`\Delta T_1 = T - 0`

`\Delta T_2 = 85 - T`

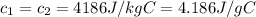
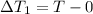
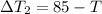
now we have

`15(333) + 15(4.186)(T - 0) = 140(4.186)(85 - T)`

`4995 + 62.79T = 49813.4 - 586.04T`

`648.83 T = 44818.4`

`T = 69^o C`