Answer:
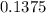 to
to

Explanation:
Given :The owner of a restaurant is reviewing customer complaints. In a random sample of 227 complaints, 57 complaints were about the slow speed of the service.
To Find :Create a 95% confidence interval for the proportion of complaints that were about the slow speed of the service.
Solution:
n = 227
x = 57
Formula of confidence for proportion:
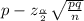 to
to
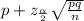
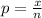


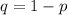
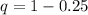
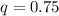
z at 95% is 1.96
Substitute the values in the formula :
Confidence for proportion:
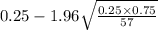 to
to
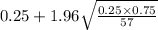
Confidence for proportion:
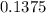 to
to

Hence 95% confidence interval for the proportion of complaints that were about the slow speed of the service is
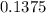 to
to
