To solve this, we have to complete the square of
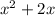
To do this with halve the
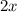 and get rid of the x, then get rid of the power on
and get rid of the x, then get rid of the power on
 , and then put them all in brackets, and the square the bracket, like so:
, and then put them all in brackets, and the square the bracket, like so:
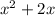 becomes
becomes
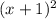
However
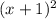 does not equal
does not equal
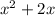
If we expand
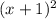 we get
we get
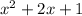 instead.
instead.
So to make it equal, all we do is subtract 1.
So when we complete the square of
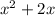 , we get
, we get
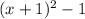
---------------------------------------------------------
So
 becomes:
becomes:
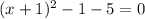
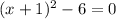
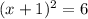
x + 1 = ±√6
x = -1 ± √6
______________________________
Answer:
x = -1 ± √6