Question

What are the values of the coefficients and constant term of 0=4-7x^2+x in standard form?

Answer 1

For this case we have that by definition, a quadratic equation is of the form:

`ax ^ 2 + bx + c = 0`

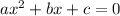
Where:

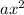`ax ^ 2`: It is the quadratic term

bx: It is the linear term

c: It is the independent term

So, if we have the following expression:

`0 = 4-7x ^ 2 + x`

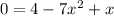
We rearrange:

`-7x ^ 2 + x + 4 = 0`

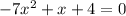
We have to:

-7: It is the quadratic coefficient

1: It is the linear coefficient

4: It is the independent term

ANswer:

-7: It is the quadratic coefficient

1: It is the linear coefficient

4: It is the independent term

Answer 2

`a=-7\\b=1\\c=4`

Explanation:

The standard form of a quadratic equation has the following formula:

`ax^2 +bx+c=0`

Where a and b are the coefficients that accompany the term x² and x and c is the constant term.

In this case we have the following equation:

`0=4-7x^2+x`

We can rewrite the equation in the following way

`-7x^2+x+4=0`

Then you can see that the values for the coefficients and constant term are:

`a=-7\\b=1\\c=4`