Question

the local independent party wants to poll registered voters to see the proportion who would consider voting for an independent candidate. how many voters they need to survey to get a 97% confidence level that the true population proportion is within a 0.03 margin of error. how many people do they need to survey to achieve the desired margin of error?

Answer 1

Answer: 1308

Explanation:

Given : Level of confidence = 0.97

Significance level :
`\alpha=1-0.97=0.03`

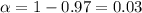
Critical value :
`z_(\alpha/2)=2.17`

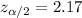
Margin of error :
`E=0.03`

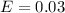
If prior proportion of population is unknown , then the formula to find the population proportion is given by :-

`n=0.25((z_(\alpha/2))/(E))^2`

`\Rightarrow n=0.25((2.17)/(0.03))^2=1308.02777778\approx1308`

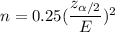
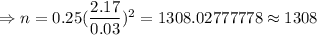
Hence, the minimum sample size needed =1308