Answer: 1.509
Explanation:
The formula of Margin of Error for (n<30):-
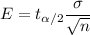
Given : Sample size : n= 22
Level of confidence = 0.99
Significance level :
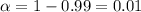
Using the t-distribution table ,
Critical value :
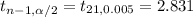
Standard deviation:
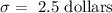
Then, we have
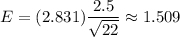
Hence, the margin of error for a 99% confidence interval for the population mean =1.509