Answer:
Option D.
Explanation:
The given function is
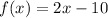
We need to find the inverse of the function f(x).
Step 1 : Substitute f(x)=y.
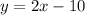
Step 2: Interchange x and y.

Step 3: Isolate variable y.

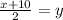
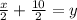
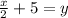
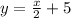
Step 4: Substitute y=h(x).
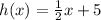
The inverse of the function f(x) is
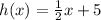 .
.
Therefore, the correct option is D.