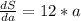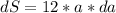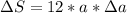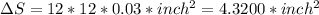Answer:
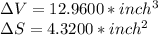
Explanation:
Hello!
In order to solve this problem we'll start by writing down the data below:
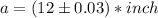
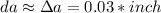
Now we are going to define two functions, the volume and the surface area of the cube in function of the measured edge a:
volume:
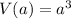
surface area:
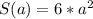
Ok so, for the maximum possible propagated error in computing the volume of the cube. We derivate V(a) and obtain:
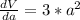
solve for dV and compute:
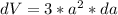

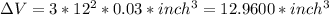
There it is for the volume...
Now we'll proceed to do exactly the same but with the function S(a):