Question

A large company is concerned about the commute times of its employees. Of the 333 employees who were surveyed, 131 said that they had a daily commute longer than 30 minutes. Create a 95% confidence interval for the proportion of employees who have a daily commute longer than 30 minutes. Use Excel to create the confidence interval, rounding to four decimal places

Answer 1

0.3409, 0.4459

Explanation:

Answer 2

Answer: (0.3409, 0.4459)

Explanation:

Given : Level of significance :
`1-\alpha:0.95`

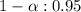
Then , significance level :
`\alpha: 1-0.95=0.05`

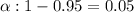
Since , sample size :
`n=333`

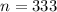
Using excel (by going in more formulas and then statistics), Critical value :
`z_(\alpha/2)=1.96`

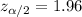
Also, the proportion of people said that they were fans of the visiting team :-

`\hat{p}=( 131)/(333)\approx0.3934`

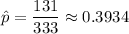
The confidence interval for population proportion is given by :-

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`0.3934\pm(1.96)\sqrt{(0.3934(1-0.3934))/(333)}\\\\\approx0.3934\pm0.0525\\\\=(0.3934-0.0525, 0.3934+0.0525=(0.3409,\ 0.4459)`

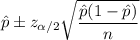
Hence, a 95% confidence interval for the proportion of employees who have a daily commute longer than 30 minutes= (0.3409, 0.4459)