Question

Consider the ODE, dy dx = y 2 1 + x (2) subject to condition y = 1 when x = 0, use your Euler code from class (modified if necessary) to find the solution to the above equation. The equation has the solution: y = 1 1 − ln(1 − x) (3) Compare the analytical and Euler result. Explain any differences

Answer 1

Computation.

Explanation:

I'm not really sure if that's the analytical solution of the inital value problem,

because y(0)=11-ln(1-0)(3)=11. Howevwer, let us procede with the given values...

Let us assume that we are going to use euler with n=2 (two steps) and h=0.2(the size of each step)

The update rules of the Euler Methode are

`X_i = X_(i-1)+h=X_0+ih`

`m_i=(dY)/(dX) \biggr \rvert_(x_i) \\\\Y_(i+1)=m_i\cdot h+y_i`

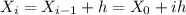
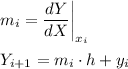
Since the initial value problem tells us that Y=1 when X=0, we know that

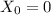`X_0=0` and that
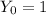`Y_0=1`. Then, we have

`X_0=0\\\\X_1=0.2\\\\X_2=0.4`

and

`Y_0=1\\\\m_0=21 \cdot Y_0 + X_0 \cdot 2=21 \cdot 1 + 0=21\\\\Y_1=0.2 \cdot 21 + 1 =5.2\\\\m_1=21 \cdot Y_1 + X_1\cdot 2=21 \cdot 5.2 + 0.2 \cdot 2=109.6\\ \\Y_2=m_1 \cdot h + Y_1 = 109.6 \cdot 0.2 + 5.2= 27.12`

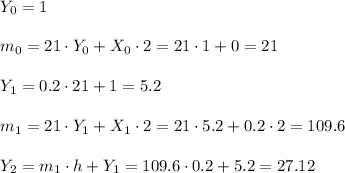
which gives us the points (0,1), (0.2, 5.2) and (0.4, 27.12).

Now, since we want to compare the analyticaland the Euler result, we first compute the value of y=11-ln(1-x)(3) for the values x=0, 0.2 and 0.4. We get that

`y(0)=11-\ln(1-0)(3)=11-ln(1)(3)=11\\\\Y(1)=11-\ln(1-0.2)(3)=11.67\\\\Y(2)=11-\ln(1-0.4)(3)=12.53`

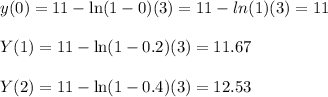
and we compute
`Y(i)-Y_i` for each i.

It holds

`Y(0)-Y_0=11-1=10\\\\Y(1)-Y_1=11.67-5.2=6.47\\\\Y(2)-Y_2=12.53-27.12=-14.59`

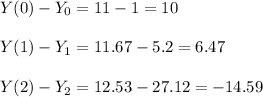
which tells us that we have a really bad approximation, as I already stated there must be a mistake in the analytical solution since the intial values don't coincide. Also note that the curve that we get using the euler methose is growing faster than the analitical solution.