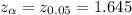Answer: 1.645
Explanation:
Given : The quality control manager of a soda manufacturing company wishes to use a significant level of 0.05 to test whether the variabilities in the amount of soda in the company's 16 OZ bottles is more than the variabilities in the company's 12 OZ bottles.
Let
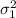 represents the variance for 16 OZ bottles and
represents the variance for 16 OZ bottles and
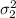 represents the variance for 12 OZ bottles.
represents the variance for 12 OZ bottles.
The Null and Alternative Hypothesis will be :-
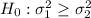
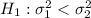 , since alternative hypothesis is left-tailed , then the test is left-tailed test.
, since alternative hypothesis is left-tailed , then the test is left-tailed test.
By using the standard normal distribution table for z, the critical value for this hypothesis:-