Answer:
Domain is all real numbers.
The range is
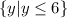
The function is increasing over
 .
.
The function is decreasing over

The function has a positive y-intercept.
-----------------This is a guess if I had interpreted your choices correctly:
Second option: The range is
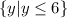
Third option: The function is increasing over
 .
.
Last option: The function has a positive y-intercept.
I can't really read some of your choices. So you can read my above and determine which is false. If you have a question about any of what I said above please let me know.
Note: I guess those 0's are suppose to be infinities? I hopefully your function is
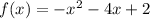 .
.
Explanation:
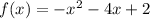 is a polynomial function which mean it has domain of all real numbers. All this sentence is really saying is that there exists a number for any value you input into
is a polynomial function which mean it has domain of all real numbers. All this sentence is really saying is that there exists a number for any value you input into
 .
.
Now since the is a quadratic then it is a parabola. We know it is a quadratic because it is comparable to
 ,
,
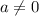 .
.
This means the graph sort of looks like a U or an upside down U.
It is U, when
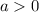 .
.
It is upside down U, when
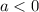 .
.
So here we have
 so
so
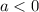 which means the parabola is an upside down U.
which means the parabola is an upside down U.
Let's look at the range. We know the vertex is either the highest point (if
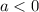 ) or the lowest point (if
) or the lowest point (if
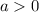 ).
).
The vertex here will be the highest point, again since
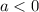 .
.
The vertex's x-coordinate can be found by evaluating
 :
:
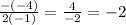 .
.
So the y-coordinate can be found by evaluate
 for
for
 :
:
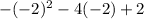
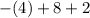
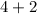
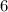
So the highest y-coordinate is 6. The range is therefore
![(-\infty,6]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4jxiiso2z36jmn1rm8cmz12v4tvxbm220c.png) .
.
If you picture the upside down U in your mind and you know the graph is symmetrical about x=-2.
Then you know the parabola is increasing on
 and decreasing on
and decreasing on
 .
.
So let's look at the intevals they have:
So on
 the function is increasing.
the function is increasing.
Looking on
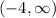 the function is increasing on (-4,-2) but decreasing on the rest of that given interval.
the function is increasing on (-4,-2) but decreasing on the rest of that given interval.
The function's y-intercept can be found by putting 0 in for
 :
:

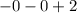
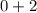
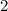
The y-intercept is positive since 2>0.