Answer: 1.467
Explanation:
Formula of Margin of Error for (n<30):-
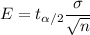
Given : Sample size : n= 22
Level of confidence = 0.90
Significance level :
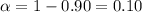
By using the t-distribution table ,
Critical value :

Standard deviation:
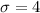
Then, we have

Hence, the margin of error for the confidence interval for the population mean with a 90% confidence level =1.467