Question

A bank offers auto loans to qualified customers. The amount of the loans are normally distributed and have a known population standard deviation of 4 thousand dollars and an unknown population mean. A random sample of 22 loans is taken and gives a sample mean of 42 thousand dollars. Find the margin of error for the confidence interval for the population mean with a 90% confidence level.

Answer 1

1.40

Explanation:

SD =4

Sample Size (n)=22

z critical value for 90%CL = 1.645

Margin of Error = z*(sd/sqrt(n))

=1.645*(4/sqrt(22))

=1.645*0.8528

=1.40 (Rounded 2 decimal places)

Answer 2

Answer: 1.467

Explanation:

Formula of Margin of Error for (n<30):-

`E=t_(\alpha/2)(\sigma)/(√(n))`

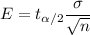
Given : Sample size : n= 22

Level of confidence = 0.90

Significance level :
`\alpha=1-0.90=0.10`

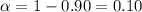
By using the t-distribution table ,

Critical value :
`t_(n-1, \alpha/2)=t_(21,0.05)= 1.720743`

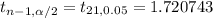
Standard deviation:
`\sigma=4`

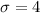
Then, we have

`E=(1.720743)(4)/(√(22))=1.46745456106\approx1.467`

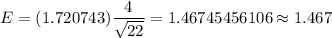
Hence, the margin of error for the confidence interval for the population mean with a 90% confidence level =1.467