Question

The average salary of a new graduate is $50,000 with a standard deviation of $6,000. The top 10% of new graduates make $57680 with probability ____

Answer 1

0.1003

Explanation:

Mean salary = u = $ 50,000

Standard Deviation =
`\sigma` = $ 6,000

Top 10% of the new graduates make a salary of $57,680. We have to find the probability that the salary of new graduate is $57,680 or more. We can find this by converting this score to equivalent z score and using the z table to find the probability of z score being higher than this value, as shown below:

The formula for z score is:

`z=(x-u)/(\sigma)`

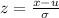
Using the values, we get:

`z=(57680-50000)/(6000)=1.28`

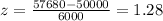
Thus,

P(Salary ≥ 57680) = P(z ≥ 1.28)

Now, using the z table, the probability of z score being higher than 1.28 comes out to be: 0.1003

So,

P( z ≥ 1.28 ) = P(Salary ≥ 57680) = 0.1003

Thus, the probability of earning a salary of atleast 57,680 is 0.1003