Step-by-step explanation:
Given that,
The distance x is in meters.
The time t is in seconds.
The velocity v is in meter/ second.
We need to calculate the SI units the constants c₁ and c₂
(A).
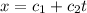
Put the unit in to the equation

Here,

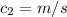
So,

(B).
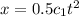
Put the unit in to the equation
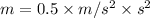
Here,
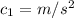
So,
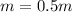
(C).
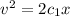
Put the unit in to the equation
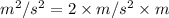
Here,
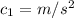
So,
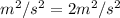
(D).

Put the unit in to the equation
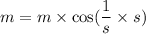
Here,


 =dimension less
=dimension less
So,

(E).
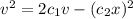
Put the unit in to the equation
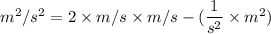
Here,
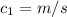

So,
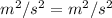
Hence, This is the required solution.