Question

For the function below, f(x) =
`(x+9)/(x+2)`,

Determine the intervals where the function is increasing. Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.
a. list any intervals on which the function is increasing ___________.
b. the function is never increasing.

Answer 1

Explanation:

Remember in order to determine the intervals where a function is increasing or decreasing we should take the derivative, a positive derivative means a function is increasing and negative derivative means a function is decreasing.

So we have the function
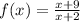`f(x)=(x+9)/(x+2)`, see this is a quotient, so we should use the quotient rule in order to find the derivative

This rule says that if you have a function
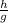`(h)/(g)` where h is the top part of the function and g is the denominator of the function, then the derivative is given by
`(h' * g - h * g')/(g^(2) )`

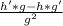
In our case the top of the function which we call h is x+9, so then the derivative of h is the derivative of x+9, since the derivative of x is 1 and the derivative of 9 is 0 we can say the derivative of x+9 is 1+0 which is just 1. So then we say h' is 1

The denominator which we call g in our case is x+2, the derivative of x is just 1 and the derivative of 2 is just 0, because 2 is a constant, so the derivative x+2 is just 1, so then we say g' is 1

So now that we know h, h' , g and g' we can plug all in the quotient rule formula
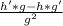`(h' * g - h * g')/(g^(2) )` and that gives us
`(1 * (x+2) - (x+9) * 1)/((x+2)^(2) )`

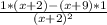
Now see that in numerator we have
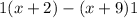`1(x+2)-(x+9)1` we can simplify that to
`x+2-x-9` , see that x and minus x would cancel and 2 - 9 is - 7 so the top becomes -7, so our derivative is
`f'(x)=(-7)/((x+2)^(2) )`

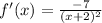
So lets analyse what we got, the top of the derivative is always -7, so it is negative no matter what we plug on x

Now looking at the denominator
`(x+2)^(2)` , see this is a function squared, remember functions squared are always positive, no matter what you plug on x, because always that we square something we get a positive result

So putting everything together, we have a numerator that is always negative and a denominator that is always positive, remember that negative divided by positive gives us a negative result. In conclusion the derivative is always negative. So according to what we said earlier, when the derivative is negative the function is decreasing, so since we got a derivative that is always negative the function is always decreasing and never increasing, so correct answer would be option B

Hope that was helpfull, good bye :)

Answer 2

Explanation:

Given is a function as

`f(x) = (x+9)/(x+2)`

Find its derivative using quotient rule.

`f'(x) = ((x+2)1-1(x+9))/((x+2)(x+2))`

Since denominator is always >0 being positive, numerator only decides about the sign of f'(x)

Numerator = x+2-x-9=-7<0 always

Hence the function does not have any interval of increase.

b) The function is never increasing.