Question

If the future value of an ordinary, 11-year annuity is $5,575 and interest rates are 5.5 percent, what is the future value of the same annuity due?

Answer 1

$5,881.63

Explanation:

The future value of an annuity is given by the formula:

`FV=PV[((1+i)^n-1)/(i)]`

Where

FV is future value

PV is present value

i is interest rate

n is the time period

The future value of annuity DUE is given by the formula:

`FV_d=PV[((1+i)^n-1)/(i)](1+i)`

Where

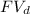`FV_d` signifies annuity due, and all other variables same

Hence we can see that the future value of annuity due has an extra multiplicative factor of (1+i) with future value of normal annuity. Since the problem tells us the FV of normal annuity is 5575, we simply multiply this by (1+i)=(1+0.055)=1.055 to get future value of annuity due.

Hence, 5575 * 1.055 = $5,881.63 (rounded to 2 decimals)